Basic terms

Support Vector

• Support vectors are the data points that lie closest to the separating hyperplane.
• Support vectors are the ones outside the tube (SVR) or exactly at the maximum margin (SVM)
• Support vectors are so called, because they support the structure or formation of the epsilon-insensitive tube or the maximum margin

Margin

= the shortest distance between the hyperplane and the closest data points (support vectors)

Soft margin

= the margin that allows misclassifications. Support vector machine (SVM) uses a soft margin.

Support Vector Regression (SVR)

=> performs regression, continuous data

Kernels SVR = non-linear

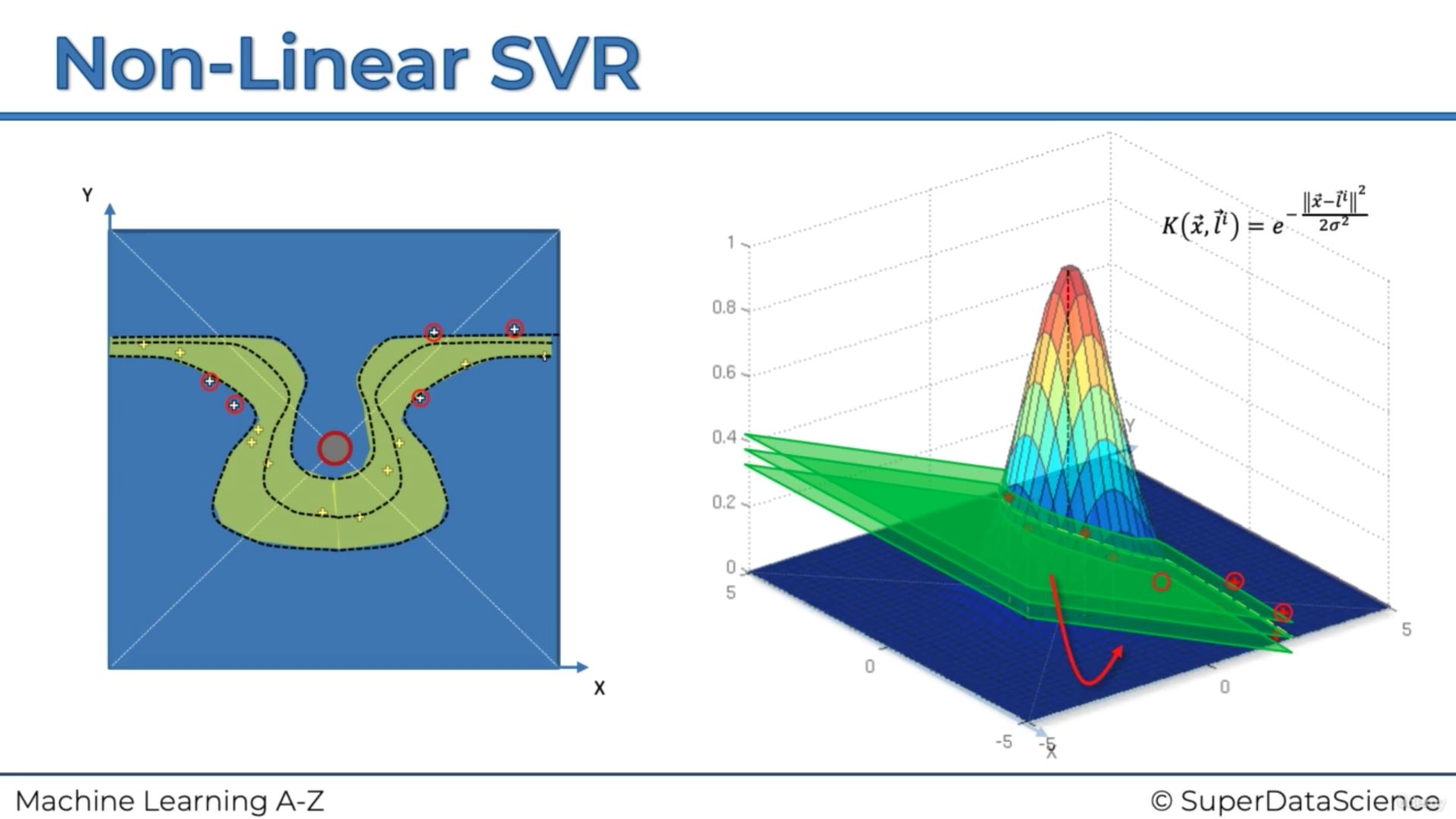
Support Vector Machine (SVM)

=> performs classification, discrete data

Support Vector Machines use Kernel Function to systematically find Support Vector Classier in higher dimension.

Kernels SVM

Why we need kernels

Kernel function is kind of a similarity measure. The inputs are original features and the output is a similarity measure in the new feature space.

Given that classification can be non-linear
=> mapping to a higher dimension (implicitly during the cost function optimization) can help:

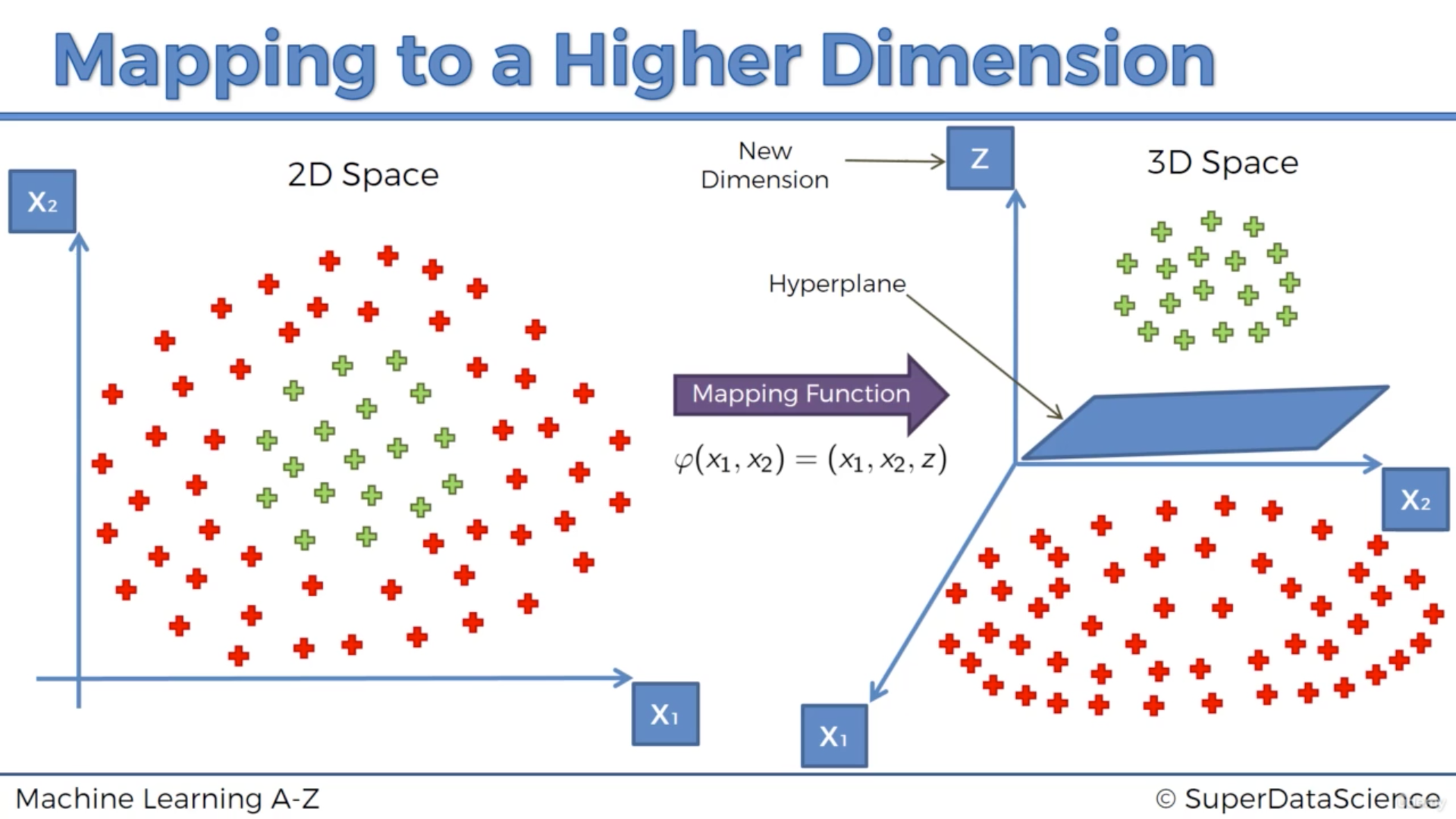
=> however, the mapping can be highly compute-intensive
=> the Kernel trick can help with that:

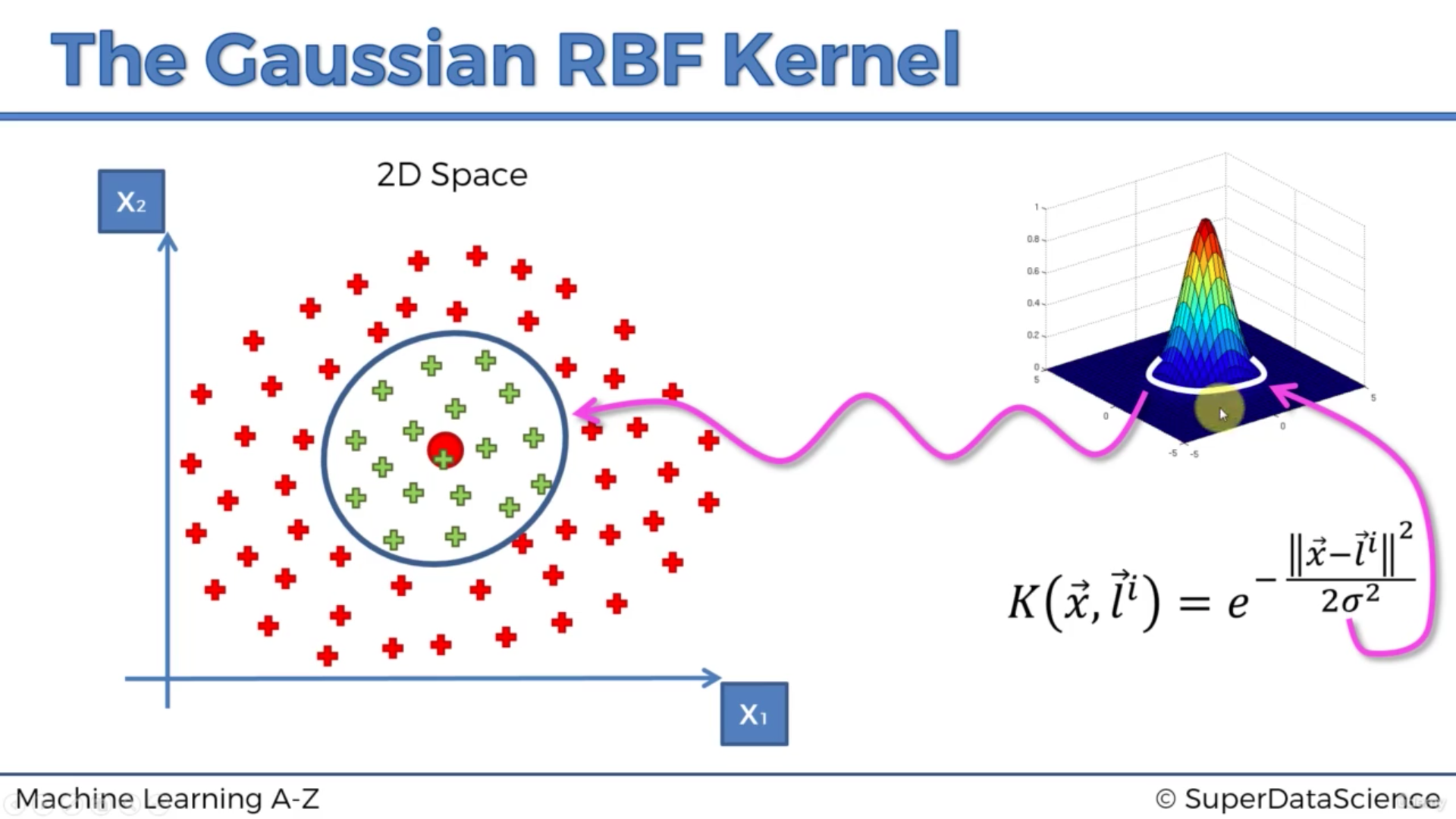
More than one kernel can be good too:

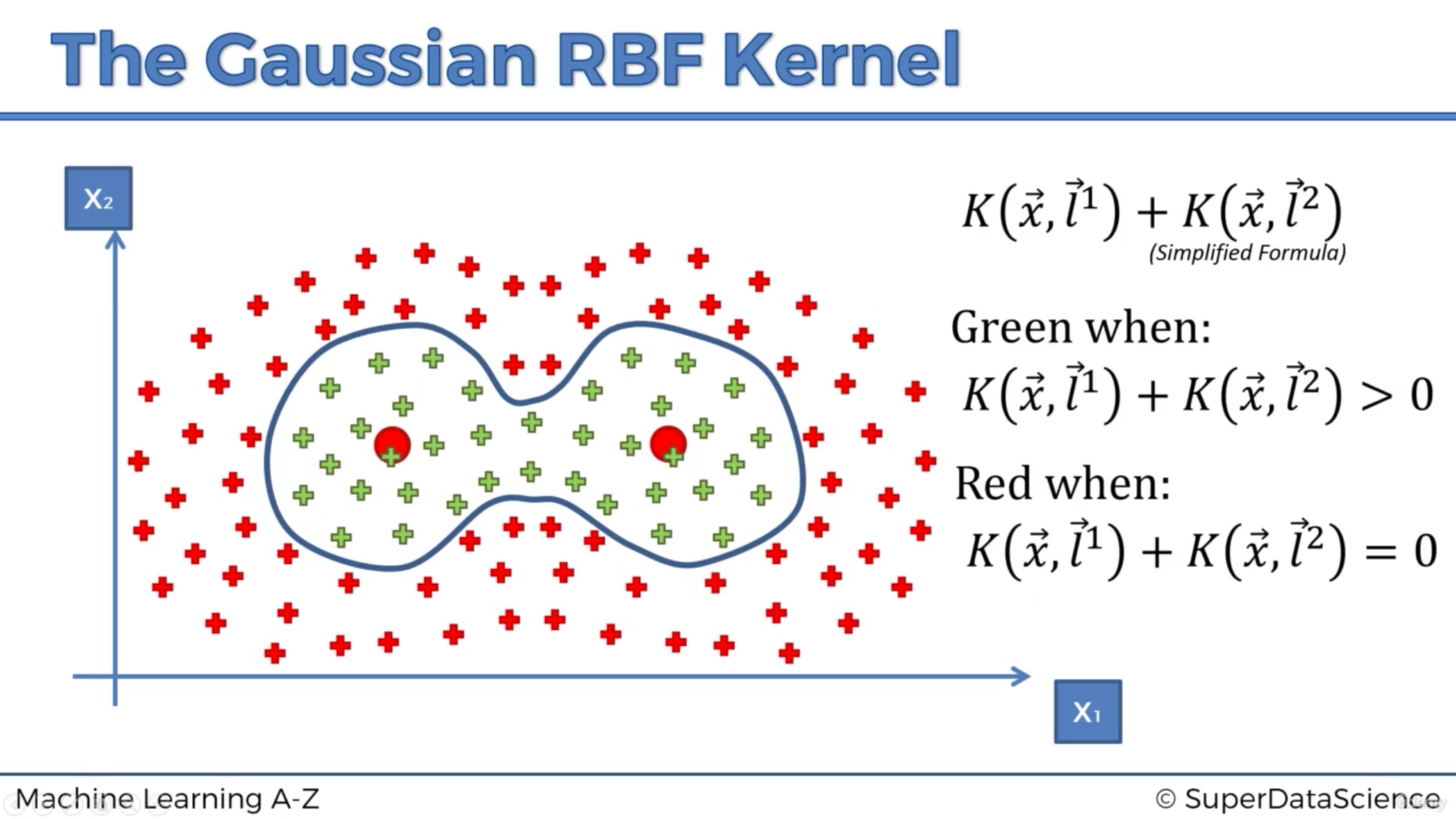
Types of Kernel Functions

• Gaussian radial basis function (RBF) Kernel
• Sigmoid Kernel
• Polynomial Kernel

Hyperparameters

• $C$: the penalty of each misclassified data (not same for all misclassified examples but proportional to the distance to decision boundary)
  • for both linear and non-linear kernel
• $gamma$: coefficient of RBF that controls the distance of influence of a single training point.
  • can be seen as the inverse of the support vector influence radius
    • low value: a large similarity radius which results in more points being grouped together.
    • high value: the points need to be very close to each other in order to be considered in the same group (or class) -> tend to overfit
  • only for non-linear model

Pros & Cons

Pros

• works well when there is a clear margin
• effective in high dimensional spaces
• effective in cases where the number of dimensions is greater than the number of samples

Cons

• not suitable for large data sets
• limited performance when the data set has more noise i.e. target classes are overlapping
• underperform when the number of features for each data point exceeds the number of training data samples